How Do You See if a Variable Has a Continuous Distribution in Stata
First off, let's start with what a significant continuous by continuous interaction means. It means that the slope of one continuous variable on the response variable changes as the values on a second continuous change.
Multiple regression models often contain interaction terms. This FAQ page covers the situation in which there is a moderator variable which influences the regression of the dependent variable on an independent/predictor variable. In other words, a regression model that has a significant two-way interaction of continuous variables.
There are several approaches that one might use to explain an interaction of two continuous variables. The approach that we will demonstrate is to compute simple slopes, i.e., the slopes of the dependent variable on the independent variable when the moderator variable is held constant at different combinations of values from very low to very high.
We will consider a regression model which includes a continuous by continuous interaction of a predictor variable with a moderator variable. In the formula, Y is the response variable, X the predictor (independent) variable with Z being the moderator variable. The term XZ is the interaction of the predictor with the moderator.
Y = b0 + b1X + b2Z + b3XZ
We will illustrate the simple slopes process using the hsbdemo dataset that has a statistically significant continuous by continuous interaction. As shown in the code below that read is the response variable, math is the predictor and socst is the moderator variable.
use https://stats.idre.ucla.edu/stat/data/hsbdemo, clear /* some descriptive statistics */ sum read math socst Variable | Obs Mean Std. Dev. Min Max -------------+-------------------------------------------------------- read | 200 52.23 10.25294 28 76 math | 200 52.645 9.368448 33 75 socst | 200 52.405 10.73579 26 71 corr read math socst (obs=200) | read math socst -------------+--------------------------- read | 1.0000 math | 0.6623 1.0000 socst | 0.6215 0.5445 1.0000
Now, let's run our regression model.
regress read c.math##c.socst Source | SS df MS Number of obs = 200 -------------+------------------------------ F( 3, 196) = 78.61 Model | 11424.7622 3 3808.25406 Prob > F = 0.0000 Residual | 9494.65783 196 48.4421318 R-squared = 0.5461 -------------+------------------------------ Adj R-squared = 0.5392 Total | 20919.42 199 105.122714 Root MSE = 6.96 ------------------------------------------------------------------------------ read | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- math | -.1105123 .2916338 -0.38 0.705 -.6856552 .4646307 socst | -.2200442 .2717539 -0.81 0.419 -.7559812 .3158928 | c.math#| c.socst | .0112807 .0052294 2.16 0.032 .0009677 .0215938 | _cons | 37.84271 14.54521 2.60 0.010 9.157506 66.52792 ------------------------------------------------------------------------------
Please note that the interaction, c.math#c.socst, is statistically significant with a p-value of 0.032.
Next, we compute the slope for read on math while holding the value of the moderator variable, socst, constant at values running from 30 to 75. To do this we will use the margins command, introduced in Stata 11, with a range of values for socst using the at option.
margins, dydx(math) at(socst=(30(5)75)) vsquish Average marginal effects Number of obs = 200 Model VCE : OLS Expression : Linear prediction, predict() dy/dx w.r.t. : math 1._at : socst = 30 2._at : socst = 35 3._at : socst = 40 4._at : socst = 45 5._at : socst = 50 6._at : socst = 55 7._at : socst = 60 8._at : socst = 65 9._at : socst = 70 10._at : socst = 75 ------------------------------------------------------------------------------ | Delta-method | dy/dx Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- math | _at | 1 | .2279094 .1424924 1.60 0.110 -.0513706 .5071894 2 | .284313 .1195771 2.38 0.017 .0499463 .5186797 3 | .3407166 .0982883 3.47 0.001 .1480752 .533358 4 | .3971202 .0799363 4.97 0.000 .240448 .5537924 5 | .4535238 .0669803 6.77 0.000 .322245 .5848027 6 | .5099274 .0628508 8.11 0.000 .3867422 .6331127 7 | .5663311 .0691477 8.19 0.000 .4308041 .701858 8 | .6227347 .0835458 7.45 0.000 .4589878 .7864815 9 | .6791383 .1026924 6.61 0.000 .4778649 .8804117 10 | .7355419 .1244141 5.91 0.000 .4916947 .9793891 ------------------------------------------------------------------------------
The values in the margins command gives the amount of change in read with a one unit change in math while holding socst constant at different values, i.e., the values are simple slopes. It appears that the simple slopes for math are significant for all values of socst except when socst equals 30.
Next, we would like to plot these simple slopes for each of the values of socst. we will use the the margins command again but place place math inside the at option. We only need two values of math for each value of socst to define the regression line for graphing purposes
margins, at(math=(30 75) socst=(30(5)70)) vsquish Adjusted predictions Number of obs = 200 Model VCE : OLS Expression : Linear prediction, predict() 1._at : math = 30 socst = 30 2._at : math = 30 socst = 35 3._at : math = 30 socst = 40 4._at : math = 30 socst = 45 5._at : math = 30 socst = 50 6._at : math = 30 socst = 55 7._at : math = 30 socst = 60 8._at : math = 30 socst = 65 9._at : math = 30 socst = 70 10._at : math = 75 socst = 30 11._at : math = 75 socst = 35 12._at : math = 75 socst = 40 13._at : math = 75 socst = 45 14._at : math = 75 socst = 50 15._at : math = 75 socst = 55 16._at : math = 75 socst = 60 17._at : math = 75 socst = 65 18._at : math = 75 socst = 70 ------------------------------------------------------------------------------ | Delta-method | Margin Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- _at | 1 | 38.07867 2.768479 13.75 0.000 32.65255 43.50479 2 | 38.67056 2.271317 17.03 0.000 34.21886 43.12226 3 | 39.26245 1.844077 21.29 0.000 35.64812 42.87677 4 | 39.85433 1.545864 25.78 0.000 36.82449 42.88417 5 | 40.44622 1.458119 27.74 0.000 37.58836 43.30408 6 | 41.03811 1.615506 25.40 0.000 37.87177 44.20444 7 | 41.63 1.959833 21.24 0.000 37.78879 45.4712 8 | 42.22188 2.412336 17.50 0.000 37.49379 46.94997 9 | 42.81377 2.923204 14.65 0.000 37.08439 48.54315 10 | 48.33459 4.100129 11.79 0.000 40.29849 56.3707 11 | 51.46464 3.459941 14.87 0.000 44.68328 58.246 12 | 54.59469 2.841761 19.21 0.000 49.02494 60.16444 13 | 57.72474 2.26369 25.50 0.000 53.28799 62.16149 14 | 60.85479 1.765578 34.47 0.000 57.39432 64.31526 15 | 63.98484 1.433357 44.64 0.000 61.17551 66.79417 16 | 67.11489 1.391418 48.23 0.000 64.38776 69.84202 17 | 70.24494 1.661882 42.27 0.000 66.98771 73.50217 18 | 73.37499 2.128836 34.47 0.000 69.20255 77.54743 ------------------------------------------------------------------------------
Now, we can plot the simple slopes using the marginsplot command introduced in Stata 12.
marginsplot, noci x(math) recast(line) xlabel(30(5)75)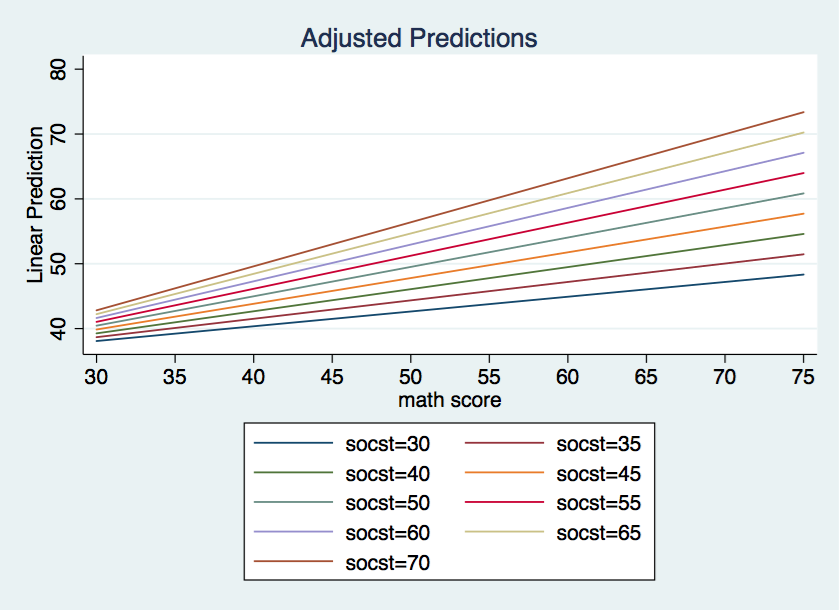
This graph is fine but it would look even better if we added in a scatterplot of the observed data points. We can do this in marginsplot using the addplot option.
marginsplot, noci x(math) recast(line) /// addplot(scatter read math, msym(oh) jitter(3)) xlabel(35(10)75)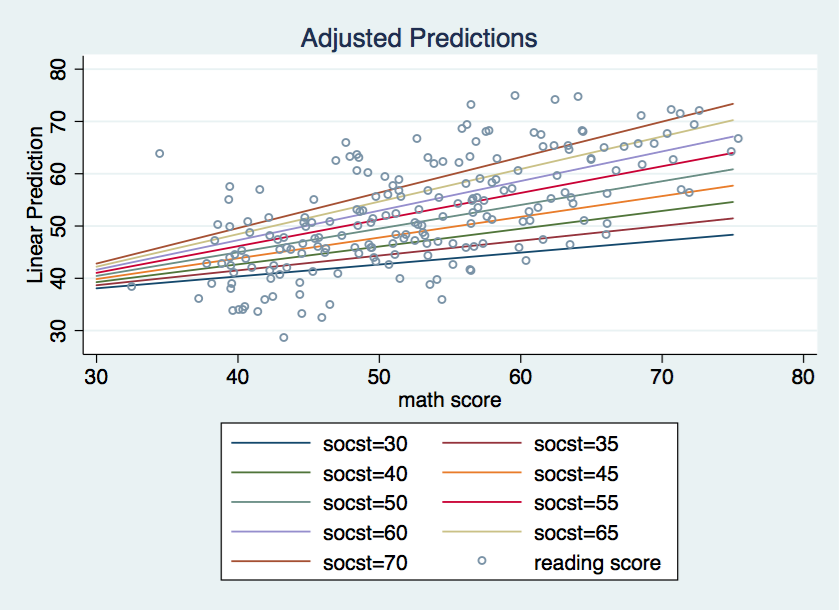
This is one way of interpreting a continuous by continuous interaction using Stata 12 and newer.
Source: https://stats.oarc.ucla.edu/stata/faq/how-can-i-explain-a-continuous-by-continuous-interaction-stata-12/